넘파이 배열
다차원 배열의 계산을 익히면 신경망을 효율적으로 구현할 수 있다.
보통 넘파이로 다차원 배열 계산을 하기에 넘파이와 다차원 배열에 대해 알아보자.
import numpy as np # 넘파이 라이브러리 불러오기넘파이 배열을 사용하려면 위 코드를 선언해주면서 넘파이 라이브러리를 불러와야 한다.
다차원 배열도 그 기본은 숫자의 집합이다.
숫자가 한 줄로 늘어선 것이나 직사각형으로 늘어놓은 것,
3차원으로 늘어놓은 것이나 N차원으로 나열하는 것을 통틀어 다차원 배열이라고 한다.
넘파이에선 array 함수를 통해 N차원 배열을 만들 수 있다.
A = np.array([1, 2, 3, 4])
print(A) # [1 2 3 4]
print(np.ndim(A)) # 1
print(A.shape) # (4,)
print(A.shape[0]) # 4
print(A.size) # 4지금까지 배웠던 1차원 배열을 넘파이를 사용해서 배열로 만들었다.
코드 함수 설명을 해보자면
배열의 차원 수는 np.ndim() 함수로 확인할 수 있다.
배열의 형상은 인스턴스 변수인 shape으로 할 수 있다.
배열의 모든 원소 수는 size 함수로 확인 할 수 있다.
shape 함수를 그냥 쓰게 된다면 결과값은 튜플로 반환된다.
이는 1차원 배열이라도 다차원 배열일 때와 통일된 형태로 결과를 반환하기 위함이다.
행렬
1차원에 1차원을 더한 2차원 배열부터는 배열이 아니라 행렬이라고 부른다.
행렬에 대한 자세한 내용은 선형대수학에서 다룰 것이기 때문에 여기선 간단하게
코드로 사용할 수 있을 정도만 알고 가도록 하겠다.
세로 배열에서 가로방향을 행 세로 방향을 열이라고 해서 행렬이 된 것이다.

2차원 배열도 코드로 구현 할 수 있다.
B = np.array([[1, 2], [3, 4], [5, 6]]) # 2차원
C = np.array([[1, 2, 3], [3, 4, 5]]) # 2차원
print(np.ndim(B)) # 2
print(C.ndim) # 2
print(B.shape) # (3, 2)
print(C.shape) # (2, 3)B는 3x2 배열이다. 3x2 배열은 행이 3개이고 열이 2개란 뜻이다.
C는 2x3 배열이다. 2x3 배열은 행이 2개이고 열이 3개란 뜻이다.
둘이 언뜻보면 다른 것 같지만 사실 같은 2차원 함수이다.
ndim 함수를 실행시키면 둘이 결과가 같은 것을 확인 할 수 있다.
D = np.array([[[[1, 2], [2, 3]], [[1, 4], [1, 3]], [[1, 2], [-2, 1]]], [[[1, 2], [2, 3]], [[1, 4], [1, 3]], [[1, 2], [-2, 1]]], [[[1, 2], [2, 3]], [[1, 4], [1, 3]], [[1, 2], [-2, 1]]], [[[1, 2], [2, 3]], [[1, 4], [1, 3]], [[1, 2], [-2, 1]]]])
D.shape # 4차원
D.size # 484차원 배열도 선언해보았다.
이렇게 N차원 배열 모두 구현할 수 있다.
[[2, 3, 4], [3, 4]] # 배열로 만든 행렬이 아닌 리스트여기까지 했으면 의문이 들 수 있다.
numpy을 이용하지 않고 위 코드 처럼 행렬을 만들 수 있는 것이 아닐까? 하는 의문이다.
그렇다면 바로 저 코드를 넘파이식으로 바꿔보도록 하겠다.
np.array([[2, 3, 4], [3, 4]]) # 열의 개수가 같지 않아 오류
np.array([[2, 3, 4], [3, 4]]).shape # (2,)이 코드를 실행시켜본다면 오류는 아니지만 경고메시지가 뜨는 것을 볼 수 있다.
VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences....
대충 이런 오류인데 열의 개수가 같지 않아서 오류가 발생하는 것이다.
shape함수도 실행시켜보면 분명 1차원 배열은 아닌데 1차원 배열처럼 나오는 것을 확인 할 수 있을 것이다.
행렬이라고 정의하는 것은 열과 행의 개수가 모두 같아야 행렬이 될 수 있다.
위 조건을 충족시킨다면 일반 배열로도 행렬을 만들 수야 있겠지만
행렬이라기 보단 리스트에 가깝고 넘파이에서 제공하는 행렬관련 함수들을 쓰지 못해 불편할 수 있다.
행렬 연산
이제 앞에서 배웠던 이런 행렬들을 가지고 행렬끼리의 연산을 배울 것이다.
행렬합
먼저 행렬합이다.
a = np.array([1, 2, 3])
b = np.array([[2, 3, 4], [3, 4, 5]])
print(a + a) # [2, 4, 6]
print(b + b)
'''
[[ 4, 6, 8],
[ 6, 8, 10]]
'''코드를 실행시켜보면 알겠지만 행렬끼리의 뎃셈이라고 해서 크게 다른 것이 없다.
그거 각 원소에 1대1 대응 시켜서 더한 것이다.
다른 형태의 행렬합은 어떨까?
print(a + b)
'''
[[3, 5, 7],
[4, 6, 8]]
'''
e = np.array([1, 2, 3, 4])
e + b # (1 x 4) + (2 x 3) 이라 계산 오류당연히 선형대수학에서 배웠던 것과 같이 오류가 날 것이라 생각했다면 오산이다.
열의 수가 같으면 계산이 가능하다.
물론 e와 b 같이 완전히 다른 두개의 행렬이 합해지는 것은 불가능하다.
행렬의 스칼라 곱
다음은 행렬에 스칼라값을 곱하는 것이다.
print(2 * b)
'''
[[ 4, 6, 8],
[ 6, 8, 10]]
'''
print(4 * b)
'''
[[ 8, 12, 16],
[12, 16, 20]]
'''
print(b * 4)
'''
[[ 8, 12, 16],
[12, 16, 20]]
'''
print(0.5 * b)
'''
[[1. , 1.5, 2. ],
[1.5, 2. , 2.5]]
'''이것 역시 우리가 알고 있는 것과 크게 달라지지 않는다.
행렬에 스칼라 값을 곱하면 각각의 원소에 1대1 대응해 곱셉이 진행된다.
그리고 교환법칙과 결합법칙이 성립하는 것을 볼 수 있다.
당연하게 실수곱도 가능하다.
행렬 기본연산
그 밖에도 여러 기본 연산들은 행렬합과 스칼라 값의 곱의 원리로 이해할 수 있다.
print(2 + b) # 덧셈
print(2 - b) # 뺄셈
print(2 / b) # 나눗셈
print(2 // b) # 몫
print(b ** 2) # 제곱
print(b % 2) # 나머지그런고로 위 연산은 실행시켜보면서 결과값을 확인해보길 바란다.
행렬곱
드디어 이 글에서 메인인 행렬곱을 배울 시간이 왔다.
행렬곱은 왼쪽 행렬의 행과 오른쪽 행렬의 열을 원소별로 곱하고 그 값들을 더해서 계산한다.
그리고 그 계산 결과가 새로운, 결과값 행렬의 원소가 된다.
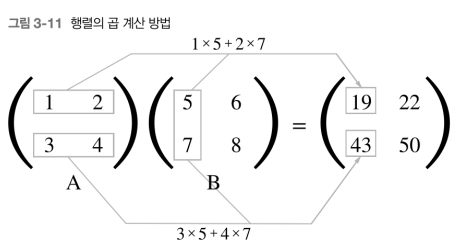
위 행렬의 곱 그림은 2x2행렬을 곱하는 방법을 보여준다.
이제 행렬끼리 곱하는 방법을 알았으니 코드로 넘어가보자.
행렬끼리의 곱은 코드로 어떻게 표현할 수 있을까?
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
print(a * b)
'''
[[ 5, 12]
[21, 32]]
'''
우선 지금까지 행렬합이 그랬듯 평소 쓰던 곱하기 기호를 써보았다.
결과값은 우리가 생각하는 것, 방금 이론으로 배웠던 행렬 곱의 결과와 다르다.
그 이유는 일반 곱하기 기호는 각 원소끼리 1대1 대응으로 곱해지는 기호이기 때문이다.
그렇다면 우리가 원하는 행렬곱은 어떤 기호로 하는 것일까
print(a @ b) # @(골뱅이)로 행렬의 곱 계산
'''
[[19, 22]
[43, 50]]
'''바로 @이 연산자로 쉽게 행렬곱을 구현할 수 있다.
또한 넘파이에서도 행렬곱셈을 해주는 함수를 제공해준다.
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print(np.dot(A, B))
'''
[[19 22]
[43 50]]
'''
print(b.dot(a))]
'''
[[23, 34]
[31, 46]]
'''
바로 넘파이 함수 np.dot()이다.
이 함수는 알아서 1차원 배열이면 벡터연산을, 2차원 배열이면 행렬 곱을 계산해준다.
그런데 위 코드를 보니 무언가 이상하다 .
dot함수를 사용하는 2가지 방법으로 계산을 해보았는데 계산 결과가 다르다.
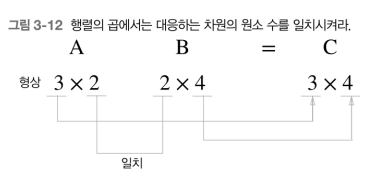
이것은 형렬의 형상에 때문이다.
구체적으로 말하면 행렬곱에서 행렬A의 1차원 원소 수와 행렬 B의 0번째 차원의 수가 같아야 한다.
이제 행렬을 사용해 아주 간단한 신경망을 구현해보겠다.
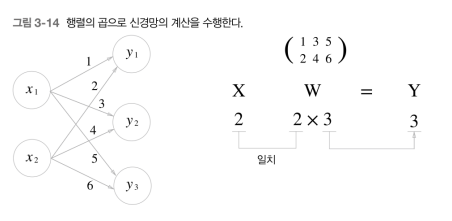
위 그림 같은 신경망을 구현한다.
X = np.array([1, 2]) # 입력값 X
print(X.shape) # (2,)
W = np.array([[1, 3, 5], [2, 4, 6]]) # 가중치 W
print(W.shape)# (2, 3)
Y = np.dot(X, W) # 출력값 Y
print(Y) # [5 11 17]이렇게 구현할 수 있다.
3층 신경망 구현
이제 좀 더 우리가 배웠던 신경망에 가까운 3층 신경망을 구현해보겠다.
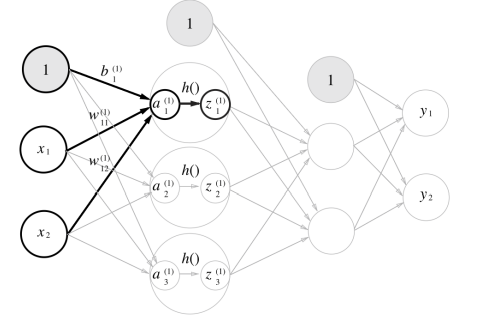
위 그림과 같은 신경망을 구현하기전에
신경망을 식으로 나타내본다.
a = w1x1 + w2+x2 + b로 나타낼 수 있다.
간소화 하면
A = XW + B가 된다.
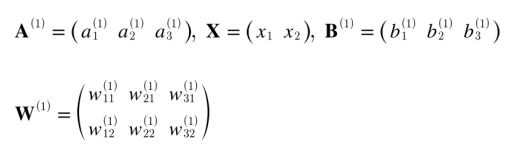
행의 각각은 다음과 같다.
넘파이 배열을 사용해서 구현한다.
3.2.4 시그모이드 함수 구현하기
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 항등함수
def identity_function(x):
return x
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x) # [ 0.31682708 0.69627909]
print(y)여기서는 init_network()와 forward()라는 함수를 정의했다.
init_network()함수는 가중치와 편향을 초기화하고 이들을 딕셔너리 변수인 network에 저장한다.
forward()함수는 입력 신호를 출력으로 변환하는 처리 과정을 모두 구현하고 있다.
그리고 이런 순방향으로 가는 신호를 순전파라고 한다.
'밑바닥부터시작하는딥러닝' 카테고리의 다른 글
| 손글씨 숫자 인식 (0) | 2023.05.25 |
|---|---|
| 신경망 (0) | 2023.05.24 |
| 퍼셉트론 (0) | 2023.05.16 |


